Time - Reversal Invariance Test at COSY
|
|
Time - Reversal Invariance Test at COSY |
|
Home : / Collaboration List TRIC for Pedestrians TRIC in Details Proposals First Results Gallery News, Theses, . . . Proposals : |
|
The TRIC-experiment is planned as a novel high-precision test of
time-reversal invariance, which conserves parity. Using the internal
circulating polarized proton beam of the COSY-ring at the
Forschungszentrum Jülich and a tensor polarized
atomic-beam target, the total cross-section asymmetry A
y,xz is to be measured with an accuracy of
10-6. The general ideas of this measurement are described
in the Proposal "Test of Time-Reversal Invariance in Proton-Deuteron
Scattering" (Proposal I ).
|
Test of Time-Reversal Invariance
in Proton-Deuteron Scattering
Proposal by:
P.D. Eversheim, F. Hinterberger, J. Bisplinghoff, R. Jahn, J. Ernst
Institut für Strahlen- und Kernphysik der Universität Bonn, Germany
J. Dietrich, O. Felden, R, Gebel, M. Glende
Institut für Kernphysik, Forschungszentrum Jülich, Germany
H. E. Conzett
Lawrence Berkeley Laboratory, Berkeley, USA
M. Beyer
Institut für Theoretische Kernphysik der Universität Bonn, Germany
H. Paetz gen. Schieck
Institut für Kernphysik der Universität Köln, Germany
W. Kretschmer
Physikalisches Institut der Universität Erlangen, Germany
We propose to perform a novel (P-even, T-odd) null test of time-reversal invariance to an accuracy of 10-4 (Phase 1) or 10-6 (Phase 2). The parity conserving time-reversal violating observable is the total cross-section asymmetry Ay,xz. The measurement is planned as an internal target transmission experiment at the cooler synchrotron COSY. Ay,xz is measured using a polarized beam with an energy above 1 GeV and a tensor polarized deuteron target.
So far, the only link to a violation of time-reversal symmetry is given via the CPT-theorem and the observation of CP-violation in the neutral kaon system. Although the CP-violation could be accomodated by a complex phase of the Kobayashi- Maskawa-matrix1) or the theta-term2) allowed by QCD, other explanations go beyond the standard model, like for instance the extension of the Higgs sector3), the superweak interaction4), or the left-right symmetric models5). These extensions of the standard model may lead to interactions that are not related to the observed CP- or T-violation. Since the origin of the CP or T-violation is not clear, further experimental tests of CP- or T-invariance outside the kaon system are necessary to probe the manifestation of the interaction responsible for the observed or possible new CP-violating effects.
In this context more direct information is expected from tests involving elementary particles compared to tests involving complex nuclei. In addition, we intend to probe the time-reversal invariance with parity being conserved in contrast to experiments which test parity and time reversal invariance (TRI) simultaneously (cf. tests of the electric-dipole moment of elementary particles).
Usually P-even TRI tests compare two observables (cf. tests of detailed balance or P A tests). Since in these experiments two observables have to be compared, the experimental accuracy6) was limited to 10-3 - 10-2. The accuracy can be increased by orders of magnitude if a true null experiment is performed i.e. a non-vanishing value of one single observable proves that the symmetry involved is violated. An example of this kind of experiment is the measurement of the parity violating quantity Az in proton-proton scattering7), which has been measured to some 10-8 (cf. Table 1). In this context the term “true” stresses the concept that the intended test has to be completely independent from dynamical assumtions. Therefore, the interpretation of the result is neither restricted nor subject to: Final state interactions, special tensorial interactions or, Hamiltonians of a certain form. True null tests are based only on the structure of the scattering matrix as determined by general conservation laws8).
It has been proven8) that there exists no true null test of TRI in a nuclear reaction with two particles in and two particles out, except for forward scattering. Based on this exception, Conzett9) could show that a transmission experiment can be devised, which constitutes a true TRI null test. He suggested to measure the total cross-section asymmetry Ay,xz of vector polarized spin 1/2 particles interacting with tensor polarized spin 1 particles.
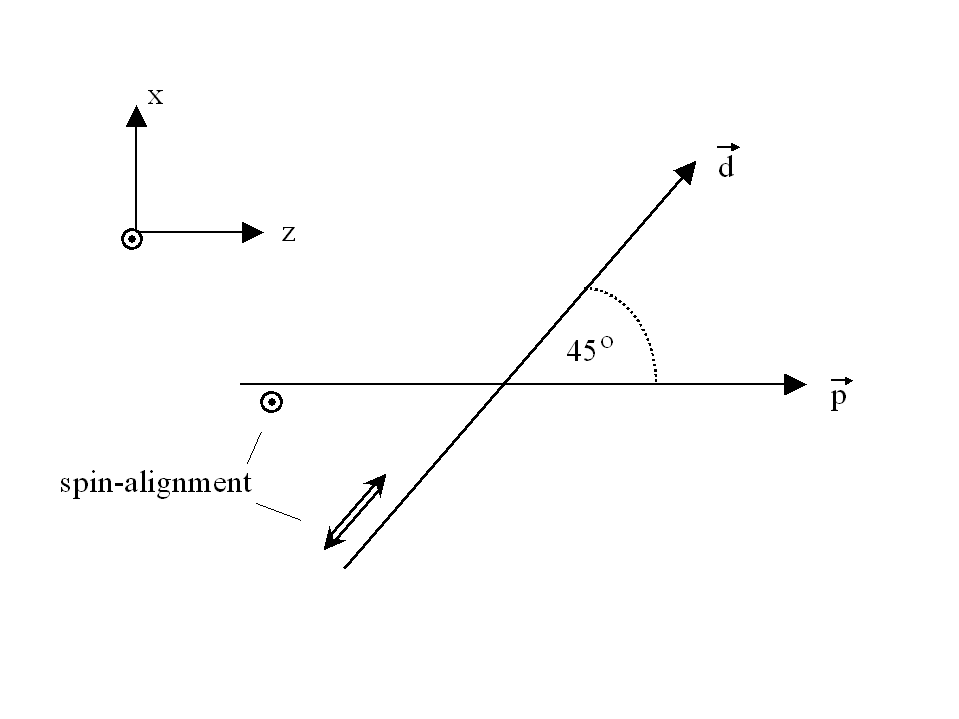
We intend to study this observable Ay,xz in the proton-deuteron system with the proton polarization Py along the y direction and the deuteron tensor polarization Pxz aligned along the x=z direction. The proton-deuteron system has the advantage of being a particularly simple system allowing still a direct analysis in terms of time-reversal violating (TRV) nucleon-nucleon potentials based e.g. on one meson exchange. In addition, the proton-deuteron system offers the opportunity to test simultaneously the p-p and the p-n interaction. According to a theorem of Simonius10), the n-p system is favoured over the p-p system as a TRI testing ground in view of the symmetry restrictions on possible TRV meson exchange processes. In principle, both systems can be tested with the intended experiment.
Table 1
Comparison of accuracies of TRI and Parity-violation tests
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
We intend to study the TRV quantity Ay,xz in a transmission experiment using an internal deuteron target in the cooler synchrotron COSY. The tensor polarized deuteron target is prepared using the polarized atomic beam target facility of the COSY experiment #5 (phase 1). Phase 2 is characterized by an improved control of systematic error contributions and the addition of a target cell to the polarized atomic beam target. The transmission losses of the circulating polarized proton beam are measured with high precision as a function of the vector- and tensor-polarization Py and Pxz, respectively. Thus, for this experiment the COSY facility is not only used as an accelerator, but also as an ideal forward spectrometer and detector.
A transmission experiment involving polarized particles is described by the generalized optical theorem18) :
|
|
|
|
|
|
|
|
|
|
|
|
The density matrix reflects the experimental set-up, whereas the scattering matrix F(0) of the forward scattering amplitudes contains the physics, which is to be tested. In the following it is shown which observable conserves parity but violates time-reversal and that the time reversed situation is tested by flipping the spin.
The discussion of parity conserving (P-even) TRV (T-odd) observable follows the arguments of Ohlsen19). It is discussed in the projectile helicity frame i.e.:
ez = ekin
with:
e is a unit vector pointing in the direction of x, y, z, kin
and kout
(2)
ey = ekin x ekout
ex = ey x ez
Since for a transmission experiment ekout is parallel to ekin, the direction of ey can be chosen at will. A convenient choice is to have ey parallel to the proton polarization Py.
In general a polarization observable describing a process of two particles having tensor polarizations of ranks r and r´ is characterized by a quantity with a number nr of indices with: nr = rin + r´in + rout + r´out. Each index specifies whether the polarization is observed in x, y, z-direction or not at all (index=0).
For the intended transmission experiment only the initial states are of interest, thus: nr = rin + r´in. Furthermore, the quantity of interest has to be invariant under the rotation about the z-axis (Rz-even). Rz invariance means to have an observable that behaves odd or even as a function of the scattering angle theta. Equivalent to this condition behaves the sum of the indices nx+ny, which is odd or even, respectively. All "odd" quantities with this respect rule out to the degree that the acceptance angle of the detector (i.e. COSY) is small. Since COSY can be tuned to have a small acceptance angle without a significant loss in luminosity, a decisive advantage over an external (spectrometer) experiment is given.
According to Ohlsen19), the symmetry character of a polarization amplitude with nr = nx+ny+nz indices can be determined by "counting rules". nx , ny , and nz are the numbers of x, y, and z indices of the observable in question. In detail the following counting rules apply for a P-even, T-odd, and Rz-even quantity:
Parity conservation : nx+ nz has to be even (3)
Rz invariance : nx+ ny has to be even
The minimal configuration fulfilling these conditions gives:
|
|
|
|
|
|
|
internal target with the thickness d and density rho |
|
|
|
For the case of polarized particles ![]() T
has to be replaced by:
T
has to be replaced by:
![]() T
=
T
=
![]() y,xz +
y,xz +
![]() Loss
=
Loss
=
![]() o
(1 + Py Pxz Ay,xz ) +
o
(1 + Py Pxz Ay,xz ) +
![]() Loss
(6)
Loss
(6)
with:
![]() o
o
![]() Loss
Loss
outside of the target
In
order to measure Ay,xz the transmission asymmetry
![]() Ty,xz
is introduced:
Ty,xz
is introduced:
|
|
Py > 0, Pxz > 0 |
|
|
i.e. either Py < 0 , Pxz < 0 |
|
|
with respect to the proton-deuteron spin-alignment |
this gives:
Is the argument of the tanh in equation (8) small, then:
With the help of equation (9) the total cross-section asymmetry Ay,xz
can be determined.
Basically, the experimental set-up only needs equipment that is provided for
other experiments, i.e. a polarized proton beam in COSY, an atomic
beam source producing polarized protons and deuterons for internal
target experiments, and an on-line current monitor20) of
high precision that is a standard diagnosis device for the operation
of COSY.
A typical measurement sequence may be:
In the following, an upper limit of the accuracy that can be achieved is
estimated from the shot noise of the scattered particles. For a two
weeks run the beam is assumed to be on target for 10 days. With an
unpolarized cross-section
Table 2
Accuracy of this experiment calculated from basic statistics for
For a conservative estimation of the accuracy that can be achieved, the
sensitivity S is introduced in equation (9):
Equation (10) defines S:
With a spin-flip every 5 s and with:
S becomes: S = 2.4 · 10-4.
The precision of the transmission asymmetry
The accuracy of Ay,xz can be further improved by increasing
the sensitivity S or by improving the precision of the
Two obvious experimental effects are discussed: i) the loss of the beam
intensity somewhere in the ring except in the target zone, and ii)
competing polarization observables.
If Ay,xz is calculated from changing the proton polarization
each time the ring is filled, all observables of Table 3 in line 1
and 5 cancel. Since only the proton polarization Py is an
eigenvector in the ring, all observables with respect to the proton
polarization Px and Pz cancel too (the average
of Px and Pz should be < 10-8 in
a 10 days run). This is true for lines 2, 4, 6, and 8 in Table 3.
In the remaining lines 3 and 7 of Table 3 all quantities with a hat
cancel, because they are not Rz-even (nx+ny
has to be even). Ay,x and Ay,yz violate parity
conservation (nx+nz is odd for these
quantities). Therefore, since p - d scattering is an elementary
process, these quantities are expected to be of the order of 10-7, even
if parity is violated. Thus, besides our quantity of interest Ay,xz,
only Ay,y "survives ".
Table 3
Polarization observables of the total cross-section in p-d scattering.
All quantities with a hat cancel, since they are Rz-odd
(nx+ny has to be even).
The latter quantity is small, because i) there must be a deuteron vector
polarization in the first place, and ii) there must be a misalignment
between the COSY beam direction and the deuteron beam, so that a
deuteron vector polarization is able to generate a Py
deuteron vector polarization. The deuteron vector polarization can be
adjusted to be zero in the atomic beam source, if this polarization
is measured in the dump of the atomic beam source. The quality by
which this is done makes the difference between phase 1 and phase 2
of this experiment.
Without major effort (phase 1), the deuteron polarization Pz can
be limited to a few percent. The deuteron source and the proton beam
can be aligned to better than 0.1o, resulting in a false
deuteron polarization Py < 10-4, which
limits the accuracy attainable in phase 1 of the experiment.
The deuteron vector- and tensor-polarization can for instance be measured
in a scattering experiment via the d+d reaction21) at 30
keV or rather by measuring the change of the atomic beam intensity
with the aid of a quadrupole-mass-spectrometer. In this case the
deuteron beam dump has to be replaced by an arrangement of two 6-pole
magnets and at least two RF-transitions (principle of an "inverted"
nuclear spinpreparation system of a ground-state atomic beam source).
Alternatively, a spin-filter can be used, which is essentially the
spin-preparation module of a Lamb-shift source. The installation of
either of these three methods provides a precise determination of the
deuteron vector- and tensor-polarization and is mandatory for phase 2
of the proposed experiment.
The precision of the standard COSY current monitors can be improved for
our purpose by an order of magnitude22), which would
improve the precision of the transmission asymmetry
Even without these improvement the quantity of interest Ay,xz
can be measured in phase 1 and phase 2 to an accuracy of 10-4
and some 10-6, respectively. The accuracy of this novel
P-even, T-odd true null test of time-reversal invariance is neither
limited by the available statistics nor the precision that can be
achieved, rather than by systematic error contributions . Below an
accuracy of 10-6 special attention has to be payed to
systematic error contributions of observables that are sensitive to
parity violation.
1) M. Kobayashi, T. Maskawa, Progr. Theor. Phys. 49 (1973)
652
2) R.J. Crewther et al., Phys. Lett. 88B (1979) 123
3) S.L. Glashow, Nucl. Phys. 22 (1961) 579
4) L. Wolfenstein, Ann. Rev. Nucl. Part. Sci. 36 (1986) 137
5) J.C. Pati, A. Salam, Phys. Rev. D10 (1974) 275
6) H.L. Harney et al., Nucl. Phys. A518 (1990) 35
7) COSY Proposal #3,
P.D. Eversheim et al., Phys. Lett. B256 (1991) 11,
S. Kistryn et al., Phys. Rev. Lett. 58 (1987) 1616
8) F. Arash, M.J. Moravcsik and G.R. Goldstein, Phys. Rev. Lett. 54
(1985) 2649
9) H.E. Conzett, 7th Intl. Conf. on "Pol. Phen. Nucl. Phys.",
Paris (1990) 2D
10) M. Simonius, Phys. Lett. B58 (1975) 147
11) N.F. Ramsey, Ann. Rev. Nucl. Sci. 32 (1982) 211
12) M. Beyer, Nucl. Phys. A493 (1989) 335 and
N.K. Cheung, H.E. Henrikson, F. Boehm, Phys. Rev. C16
(1977) 2381
13) C.F. Hwang et al., Phys. Rev. 119 (1960) 352
14) E.Blake et al., Phys. Rev. Lett. 51 (1983) 355
15) V.E. Bunakov, Phys. Rev. Lett. 60 (1988) 2250
16) Y. Yamaguchi, J. Phys. Soc. Jpn. 57 (1988) 1518
17) M. Beyer, Nucl. Phys. A560 (1993) 895
18) C. Bourrely, E. Leader, J. Soffer, Phys. Rep. 59 (1980)
95; note that their equation (3.41) is not the most general one,
since rho is in general not a real matrix
19) G.G. Ohlsen, Rep. Progr. Phys. 35 (1972) 717
20) K.B. Unser, CERN/SL/90 27 (BI)
21) B. Polke et al., 7th Intl. Conf. on "Pol. Phen. Nucl.
Phys.", Paris (1990) 57B,
and H. Paetz gen. Schieck, private communications.
22) Private communications, S. Vigdor IUCF Bloomington, USA and P. von Rossen
COSY Jülich, Germany
![]() Ty,xz
=
- tanh
(
Ty,xz
=
- tanh
(![]() o
· rho · d · N Py Pxz Ay,xz )
(8)
o
· rho · d · N Py Pxz Ay,xz )
(8)
![]() Ty,xz
=
-
Ty,xz
=
- ![]() o
· rho · d · N Py Pxz Ay,xz
(9)
o
· rho · d · N Py Pxz Ay,xz
(9)
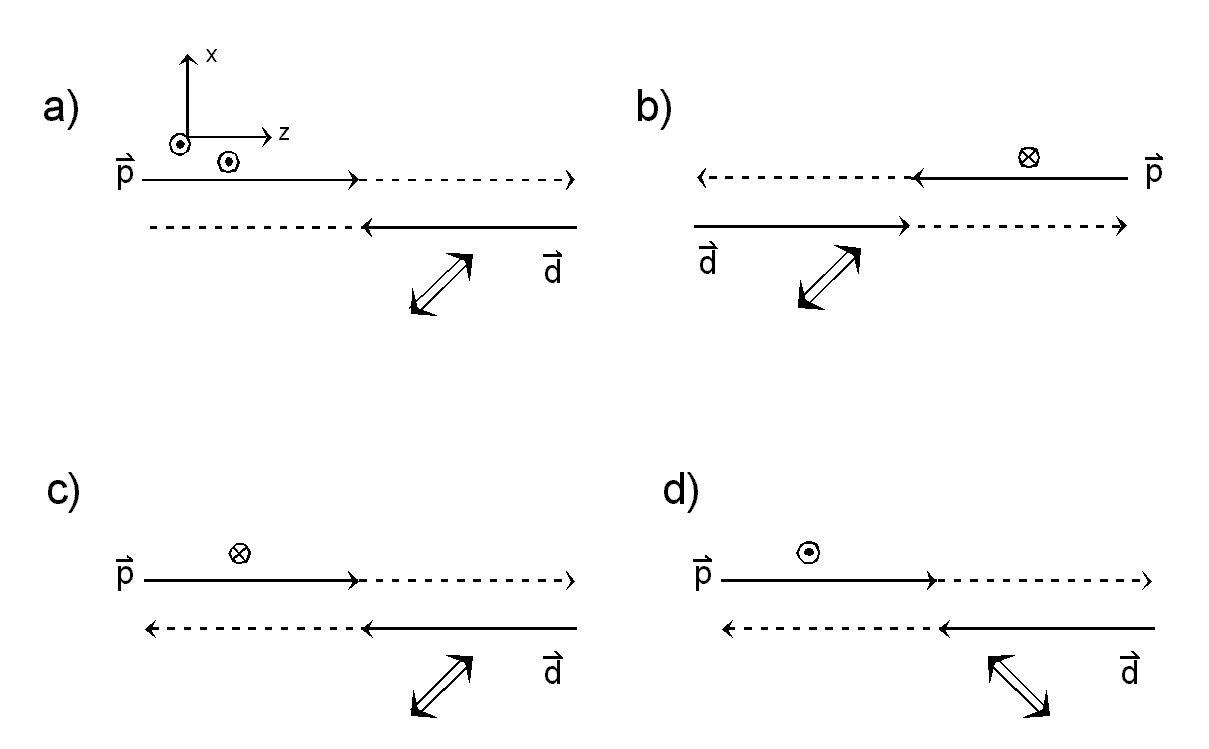
Fig. 2
Pictorial demonstration that a time-reversed situation is prepared by either a
proton or a deuteron spin-flip. a) The basic system is shown. b) The
time reversal operation is applied (momenta and spins are reversed
and the particles are exchanged). In order to have a direct
comparison between situation a) and b), two rotations Ry
(Pi) or Rx(Pi) by 180o about the y- or x- axis are
applied, leading to the situations c) and d), respectively. This is
allowed, since the scattering process is invariant under rotations.
![]()
![]()
![]()
The Accuracy of the Experiment
![]() o
= 80 mb the following
accuracies for various beam intensities and target thicknesses are
calculated (Table 2):
o
= 80 mb the following
accuracies for various beam intensities and target thicknesses are
calculated (Table 2):
phase 1 (rho· d = 1012 atoms/cm2) and phase 2
(rho·d = 4·1014 atoms/cm2)
![]() Ty,xz
=
- S · Ay,xz
(10)
Ty,xz
=
- S · Ay,xz
(10)
![]() o
· rho · d · N Py
Pxz
(11)
o
· rho · d · N Py
Pxz
(11)
![]() o
o
![]() Ty,xz is
calculated from the precision of the current measurement. For 1.3 ·
1011 protons in the COSY ring the current is measured
within 40 ms to a precision of 5 · 10-5. Within 10 days
the precision of the transmission asymmetry
Ty,xz is
calculated from the precision of the current measurement. For 1.3 ·
1011 protons in the COSY ring the current is measured
within 40 ms to a precision of 5 · 10-5. Within 10 days
the precision of the transmission asymmetry ![]() Ty,xz is
measured to 1 ·10-8. With equation (10) the accuracy delta Ay,xz
of the total-cross-section asymmetry Ay,xz is
calculated: delta Ay,xz = 4 ·10-5.
Ty,xz is
measured to 1 ·10-8. With equation (10) the accuracy delta Ay,xz
of the total-cross-section asymmetry Ay,xz is
calculated: delta Ay,xz = 4 ·10-5.![]() Ty,xz
measurement. The sensitivity can be improved by extending the
spin-flip period, for instance from 5s to 50s. As a consequence the
number of turns N and hence the sensitivity S is increased by an
order of magnitude. In case the precision of the current measurement
is improved simultaneously by an order of magnitude the
precision of
Ty,xz
measurement. The sensitivity can be improved by extending the
spin-flip period, for instance from 5s to 50s. As a consequence the
number of turns N and hence the sensitivity S is increased by an
order of magnitude. In case the precision of the current measurement
is improved simultaneously by an order of magnitude the
precision of
![]() Ty,xz
is improved accordingly, and delta Ay,xz
reduces to 4·10-7. Under these conditions
delta Ay,xz is dominated by the shot noise of the underlying
statistics of the scattering process, and it becomes increasingly
important to discuss in more detail the handling of systematic
errors.
Ty,xz
is improved accordingly, and delta Ay,xz
reduces to 4·10-7. Under these conditions
delta Ay,xz is dominated by the shot noise of the underlying
statistics of the scattering process, and it becomes increasingly
important to discuss in more detail the handling of systematic
errors.
The first index refers to the proton polarization, the second and third index refers to the
deuteron vector- and tensor polarisation.
![]() Ty,xz
measurement accordingly. The precision of the standard COSY current
monitors is limited by the Barkhausen noise of its ferrits. Using the
fast pick-up devices of the stochastic cooler tanks of COSY with its
cooled FET-amplifiers provides lower noise current monitors.
Moreover, because there are several such devices placed about the
COSY ring, the precision of the current measurement can be improved
further.
Ty,xz
measurement accordingly. The precision of the standard COSY current
monitors is limited by the Barkhausen noise of its ferrits. Using the
fast pick-up devices of the stochastic cooler tanks of COSY with its
cooled FET-amplifiers provides lower noise current monitors.
Moreover, because there are several such devices placed about the
COSY ring, the precision of the current measurement can be improved
further.
Proposal for
Measurement
of the Total
![]() Correlation Coefficient Ay,y
Correlation Coefficient Ay,y
by the TRIC Collaboration
In view of the proposed Test of Time-Reversal Invariance (TRI) in Proton-Deuteron Scattering [1-8] at COSY (proposal #22) the measurement of the dominant error contributions is decisive for the accuracy of the TRI experiment. In the TRI proposal it is argued that the total correlation coefficient Ay,y is the only observable in proton-deuteron scattering, which can fake a TRI effect.
Since the total correlation coefficient Ay,y is not known at 1 GeV which is the proposed energy for the TRI test Ay,y has to be determined. The experiment is to take place at TP2 and thus the EDDA detector can be used as an internal polarimeter. Ay,y shall be measured in two ways:
i) The circulating polarized proton beam at 1 GeV interacts with the polarized deuteron beam from the atomic-beam target for EDDA [6,9]. Asymmetries with respect to the spin configuration of the beam and the target are measured over the total angular acceptance of the EDDA detector.
ii) The measurement is performed by observing the decrease of the circulating current in COSY as a function of the spin alignments of the beam and the target (this method is described in detail in the TRI proposal #22 [1])
Method i) is very useful for studying systematic errors of the measuring principle. Since the angular acceptance of the EDDA detector does not cover completely 180o and the elastic channel is preferentially analysed, Ay,y is only approximately determined.
In
contrast, method ii) measures all inelastic channels and regards the
complete angular range from 0o-180o, since the
forward scattering amplitude is measured via the transmission
asymmetry
![]() Ty,y.
Ty,y.
![]() Ty,y
contains Ay,y, the quantity of interest for this
experiment in the same way as Ty,xz contains Ay,xz,
the quantity of interest for the TRI test (cf. the TRI proposal ).
Thus a novel type of internal experiment will be established that
utilizes the COSY ring not only as an accelerator but also as an
ideal forward spectrometer and detector.
Ty,y
contains Ay,y, the quantity of interest for this
experiment in the same way as Ty,xz contains Ay,xz,
the quantity of interest for the TRI test (cf. the TRI proposal ).
Thus a novel type of internal experiment will be established that
utilizes the COSY ring not only as an accelerator but also as an
ideal forward spectrometer and detector.
The apparatus for method i) is the usual EDDA set-up with a special RF-transition for the polarized atomic-beam target, which provides a vector polarized deuteron beam (Pz = 1) This transition has been developed in the diploma thesis of Dirk Lorenser, University Bonn. Since only weak holding fields across the interaction zone are allowed at COSY, a pure deuteron state has to be prepared. This in turn implies that simultaneously the atomic deuteron beam will be tensor polarized (Pzz = 1). On the other hand, switching off the RF-transitions provides a deuteron beam with Pz = 1/3 and Pzz = –1/3 at the exit of the target. The holding field is vertically aligned so that the vector- and tensor-alignment is adiabatically changed to Py and Pyy at the interaction zone.
Since the holding field is provided by ferrite cored electric magnets, a fast spin-flip (< 1ms) can be provided. Switching off the RF-transition gives a different linear combination of deuteron vector- and tensor-polarization. Finally, interspersing sequences with an unpolarized proton beam, allows to extract Ay,y. In more detail, according to Ohlsen [10], for a vertical holding field, the following quantities are of interest:
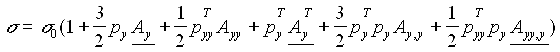 (1)
(1)
with:
If the Left-Right asymmetries
are not measured with the EDDA detector, all underlined quantities do
not contribute. Providing an unpolarized proton beam with the
flipping of the holding field and the RF-transition switched on- and
off, allows to determine Ayy and
Since for method i) it has
been shown that by proper combinations of spin flip and switching on-
and off the RF-transition the total amount of scattered particles is
changed, the transmission is changed accordingly. Therefore, Ay,y
can be deduced from a transmission asymmetry too.
![]() ,
,![]()
![]() . Then, with a polarized proton beam, Ay,y the quantity
of interest can be determined as soon as the proton spin is flipped.
. Then, with a polarized proton beam, Ay,y the quantity
of interest can be determined as soon as the proton spin is flipped.
Given a cross-section of 80 mb, a target density of 2·1011 deuterons/cm2, an intensity of 1010 polarized protons circulating at 1 MHz, results in a total rate of 160 Hz. Under these conditions for the scattering experiments some hours should be sufficient for a precision of some percent.
The TRIC collaboration is asking for 6 days of beam-time splitted in 2 periods of 3 days each. These periods should preferably be scheduled following a beam development week. The time is intended for the following purposes:
Especially: a) Study the quality of the deuteron polarization.
b) Study the quality of the polarized proton beam
c) Study systematic error sources
2) Establish a novel measuring technique for a ring-accelerator. Use the EDDA detector as an efficient polarimeter and luminosity monitor.
1) COSY Proposal #22: “Test
of Time-Reversal Invariance in Proton-Deuteron
Scattering”
2) P.D. Eversheim
Proc. of the 2nd Adriatico Research Conf. on Pol. Dynamics in Nuclear and
Particle Phys., Triest, Italy, World Scientific (1992)
142
3) P.D.
Eversheim, F. Hinterberger, J. Bisplinghoff, R. Jahn, J. Ernst, W.
Kretschmer, H. Paetz gen. Schieck, and
H.E. Conzett AIP Conference Proceedings 339 (1994) 191
4) P.D. Eversheim
Int. Workshop on Pol. Beams and Pol. Gas Targets, Cologne,
Germany
World Scientific (1996) 224
5) P.D. Eversheim,
F. Hinterberger, J. Bisplinghoff, R. Jahn, J. Ernst, M. Beyer,
H. Paetz gen. Schieck, W. Kretschmer and
H.E. Conzett
12th Int. Symp. on High-Energy Physics, Amsterdam, The Netherlands
World Scientific (1996) 303
6) P.D. Eversheim, M.
Altmeier, and O. Felden
Nucl. Phys. A626 (1997) 117c
7) P.D. Eversheim, F.
Hinterberger, J. Bisplinghoff, R. Jahn, J. Ernst, H. Paetz gen.
Schieck, W. Kretschmer, and H.E. Conzett
AIP Conference Proceedings 421 (1997) 501
8) P.D. Eversheim
Nucl. Phys. A629 (1998) 471c
9) P.D. Eversheim, M.
Altmeier, O.Felden, M. Glende, M. Walker, A. Hiemer, and
R. Gebel
AIP Conference Proceedings 421 (1997) 419
10) G.G. Ohlsen
Rep.Prog.Phys.
35 (1972) 760
|
|
|
|